作者:华山派小6
在中学里,我们已经知道:许多常见的平面几何图形都可以用代数方程来描述。比如单位圆周(即以原点为圆心且半径为1 的圆周)的方程是 . (*)具体来说,单位圆周上每个点P可以用一对实数(
,
)来表示(称为坐标),它们满足关系式(*); 反过来,所有满足该关系式的数组(
,
)都对应单位圆周上的点。
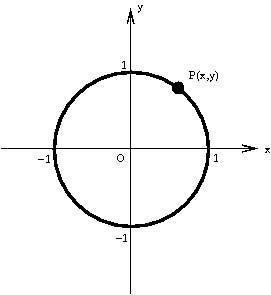
图1
一个有趣的问题是:如果将和
的取值范围扩大到复数情形,那么这个图形会变成什么样呢?
为了回答这个问题,我们首先来解释复数是什么。容易看到,方程 在实数范围内是没有解的。这是因为任何实数的平方总是大于等于零。尽管如此,我们可以模仿实数情形的开根运算,强制定义该方程的两个解:
那么
是否真正有意义呢?为了说明它有意义,就必须选择一种直观的方式让人们能够“看到”它。当我们谈论
或者
等等具体实数时,它们总可以被解释成面积为2或者5 的正方形的边长。但是
却不能用这种直观方式来解释。因为你无法说清楚一个面积为-1的正方形是什么。所以这种方式还不足以让我们“看到”
的模样。
因此我们必须寻找其他方法来解释. 事实上,实数本身就有一种直观的解释:它们可以看成直线上的点(反之亦然)。那么
是否可以看成平面上的点呢?这个想法来自于大数学家高斯。他把平面上的每个点(
,
)看成一个新的“数”
这样,
恰好对应平面上的坐标点(0,1);而每个实数则恰好对应
轴(图2 的水平直线)上的点。为了书写方便,
传统上记为字母
, 被称作虚数单位。
被称为复数。
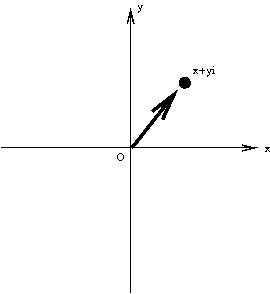
图2
这样一来,复数就变得和实数一样直观了。所有的复数放在一起构成了一个比实数集合更大的数系。从上面的几何解释来看,实数集合相当于一条直线(叫做实数轴),而复数集合则是整个平面(叫做复平面)。此外,人们也能在复数上建立起加减乘除四则运算,它们保留了实数运算的所有规律。
你可能会想,既然方程 创造了复数,那么其他代数方程(比如
等等)是否会创造出其他与众不同的“新”数呢?高斯给出了否定回答。他断言,任何形如
的方程的解都只能是复数(这里诸
是你事先取定的复数)。从这个意义上说,复数集合是最大的数系了。
现在回到一开始的问题上。当我们把点(,
)中的分量
,
的取值范围扩大到复数集合时,原来的平面显然已无法容纳这样的点了。因此我们需要把平面扩大到维度更高的空间里(就像刚才把实数轴扩大到复平面一样)。因为
,
现在是复数,所以我们不妨把它们写成
(
,
)的全部信息实际上是由实数组(
,
,
,
)完全确定的。反过来,任取四个实数,当然也能得到(
,
) . 仿照平面的作法,我们可以构建一个四维空间。这个空间中的点可以由实数组(
,
,
,
)来确定。这样一来,(
,
)就可以看成是四维空间里的点。
我们考虑那些满足 的数组(
,
) . 首先,根据上面的讨论,它们被置于四维空间(
,
,
,
)中。我们要做的就是找出这四个量
,
,
,
之间的关系。只须将(**)代入到上述方程中就可以得到
为了让左边的复数和右边的1 相等(把它们看成复平面上的点比较一下),则必须有
这就是它们之间必须满足的关系式。由于四个变量
,
,
,
要同时满足两个方程,因而其中有两个变量能被剩下的两个变量表示出来(尽管我们未必能写出明显的表达式)。这就表明,满足
的点组成的几何图形在四维空间中构成一个曲面!这里的曲面就是我们通常说的二维几何物体(想象一下你见过的皮球和救生圈等等的表面)。
接下来的问题当然是如何“看到”这个曲面。遗憾的是,我们无法在现实世界中呈现四维空间,所以你不可能在四维空间里直接观察这个曲面。尽管如此,我们仍然可以通过数学手段去考察它。比如,利用拓扑和复分析的工具,可以发现这个曲面应该形如一个皮球(可能有点瘪)。
图3
当然,如果你真想看到它的样子,也是有办法的,只是要付出些代价。比如我们可以把四维空间压缩成三维空间(想像把一个易拉罐压扁的情形)。这样一来,四维空间中的曲面就变成了三维空间中的曲面。但是这种压缩往往是有副作用的:它会把曲面压坏掉,使得曲面上出现一些“褶皱”。这种“褶皱”在现实世界的三维空间中是不可能出现的。
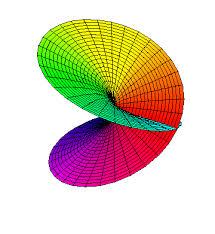
图4
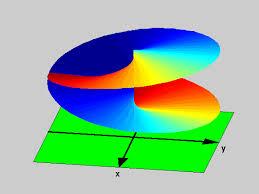
图5
比如上述两幅图都是该曲面压缩到三维空间中的局部示意图。它看上去像是上下两圆盘在某条“褶皱”处彼此穿越过对方而连接起来。如果是在现实世界中,这种穿越必然导致圆盘在褶皱处撕裂开一条缝,以便让其中一个圆盘能够穿过去。但事实上,这样的裂缝并不存在。
那么这样的曲面和原先的单位圆周之间是什么关系呢? 我们看到,原始的实数坐标点(,
)相当于四维空间中的点(
,0,
,0) . 这种点构成的几何图形是四维空间中的一个平面(类似于你的桌面,只不过它悬浮在四维空间中)。因此,我们看到的单位圆周只不过是这个曲面和该平面交截出的曲线而已(见图6)。
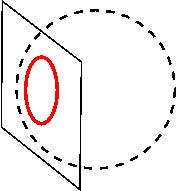
图6
这多少会让人联想起“盲人摸象”的典故。我们在实数平面上看到的单位圆周其实只不过是“大象”的鼻子,而真正的“大象”(即这个曲面)却躲藏在平面之后的四维空间中。
上面的例子自然也会启发人们去考虑更一般的方程,比如 或者
等等。可以想象,它们在复数域的情形下也会变成四维空间中的曲面,而你在实平面看到的相应曲线只不过来自于它们和某个四维空间中的平面的交截。例如下面的两组实平面上的三次曲线
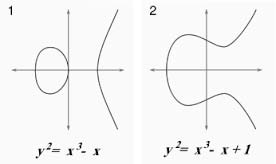
图7
它们在四维空间里的真实图形应该是一个救生圈(可能有点瘪)。
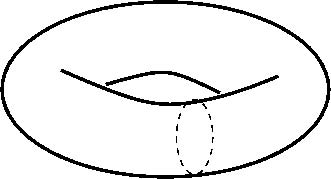
图8
原先的实曲线其实是这样截出来的:
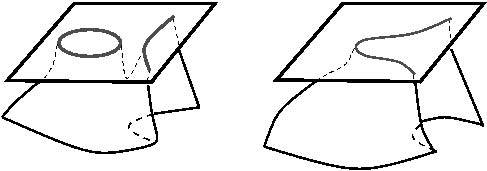
图9
这就类似于潜伏在海平面下的冰山。你所看到的不过是露出海面的冰山一角。
一般的代数曲线——即由关于,
的多项式方程所描绘的几何图形——在四维空间中的图形都是这样的曲面。只不过有些曲面可能在四维空间中会被挤坏,出现一些尖锐的点。比如
对应的曲面就包含这样的点。
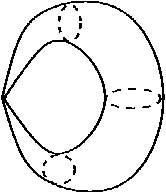
图10
只要把它们送到更高维的空间中舒展开,就有办法去掉这些挤坏的点。这样,我们最终可以得到如下的曲面(下图是它们在三维空间中的模型)

图11
这些曲面被称为黎曼曲面。它们看上去就像含有若干个“洞眼”的甜甜圈。“洞眼”的个数叫做亏格。它是反映这个黎曼曲面本性的数值量。
黎曼曲面是代数几何中最基本的研究对象之一。许多数学分支都和它有着千丝万缕的联系。比如平面解析几何中的圆锥曲线对应亏格0 的黎曼曲面(即球面)。又比如著名的椭圆曲线就是亏格1 的黎曼曲面(即环面),它和费马大定理、密码理论等等都有着深刻的关联。
附录:
图4 链接:
图5 链接:
图7 链接:https://www.quora.com/How-would-you-explain-elliptic-curves-to-a-layperson
图11 链接:http://www.map.mpim-bonn.mpg.de/2-manifolds


