把一条细长纸带对折,接着把对折后的纸带再对折,又再对折,重复这样的对折几十次,然后松开纸带,从纸带侧面看过去,我们得到是一条弯弯曲曲的折线。请别小看这个连小孩子都会做的游戏。从它开始,我们可以探索一连串现代科技中耳熟能详的名词:分形、混沌、蝴蝶效应、生命产生、系统科学……
我们把‘纸带对折一次’的动作,对应于几何图形中的一次‘迭代’,如刚才所描述的循环往复的‘迭代’操作所得到的最终图形叫做中国龙,或称分形龙。下图描述了分形龙曲线的生成过程:
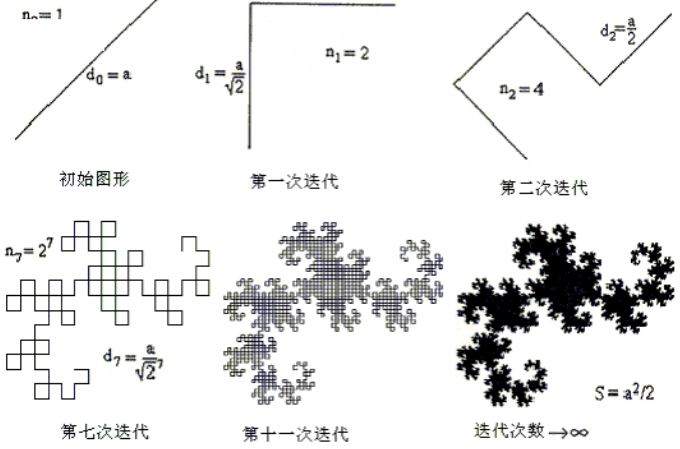
图一
仔细研究上图中分形龙的产生过程,可观察到如下三个有趣之处:
1. 简单的迭代,进行多次之后,产生了越来越复杂的图形;
2. 越来越复杂的图形表现出一种‘自相似性’;
3. 迭代次数较少时,曲线看起来是一维折线,此曲线随着迭代次数的增加而逐渐充满部分平面。
第一条特点一目了然,无需多言。
第二条的‘自相似性’是什么意思呢?那是说:一个图形的自身可以看成是由许多与自己相似的,大小不一的部分组成的。最通俗的‘自相似’例子是中国人喜欢吃的花菜,花菜的每一部分,都可以看成是与整棵花菜结构相似的‘小花菜’。分形龙曲线也具有这种‘自相似性’,从下面的图中可以看出:分形龙可以看成是由四个更小的但形状完全一样的‘小分形龙’组成的。
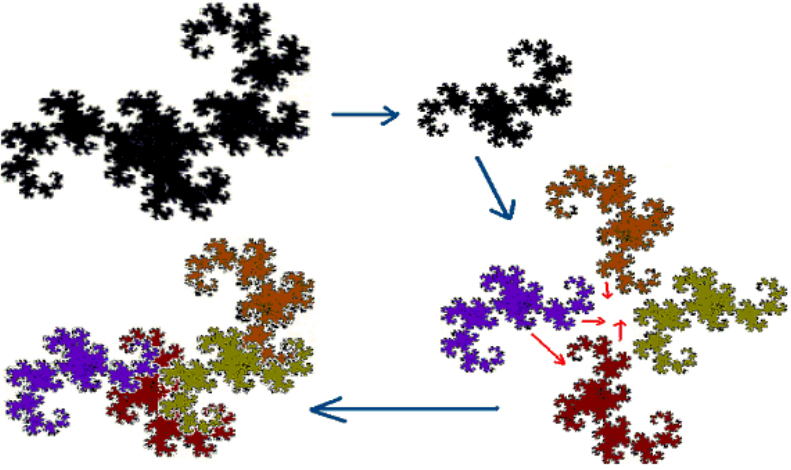
图二
上述的第三条特点是有关图形维数的变化:一维的折线随着迭代次数的增加,逐渐充满部分平面,看起来变成了二维图形。
谈到几何图形的‘维数’,我们不能只凭感觉了,需要更多的数学论证。
分形龙是分形的一个特例,不同的迭代方法,可以形成各种各样不同的分形,对分形的研究,形成一个新的几何分支:分形几何。
其实,在‘分形’这个名字中,就已经包含了‘分数维数’的玄机。众所周知,经典几何学中,有1维的线、2维的面、3维的体。三维以内,有现实物理世界的物体对应,容易理解,维数大于三的时候,就需要应用一点想象力了,比如加上了时间的四维空间等。但是不管怎么样,经典几何的‘维数’总是一个整数。而分形几何中的‘维数’则包含了‘分数维’,这就是‘分形’名称的来源。如何理解分数维?首先,我们从几个例子来说明这个分数维的概念。
在经典几何中,用拓扑的方法来定义”维数”,也就是说,空间的”维数”等于决定空间中任何一点位置所需要变量的数目:比如,所谓‘三维’,是因为我们需要三个数值来确定一个物体在空间的位置。对于一个二维空间,比如球面,则需要俩个数值来确定一个物体的位置。当汽车行驶在一条高速公路上,它的位置可以用一个数:出口的序号数,来表示。这是一维空间的例子。显然,按照这种拓扑方法定义的”维数”,只能是整数。
在分形几何中,我们将拓扑方法定义的‘维数’,扩展成用与自相似性有关的度量方法定义的‘维数’。刚才我们已经介绍了花菜结构和分形龙的‘自相似性’,其实,经典整数维的几何图形,诸如一条线段、一个长方形、一个立方体,也具有这种‘自相似性’,比如说,如下图所示:(a)一条线段是由两个线段接成的;(b)一个长方形,可以被对称地剪成四个小长方形,每一个都与原长方形相似;(c)一个立方体,可以被对称地切成八个小立方体,每一个也与原立方体相似。只不过对经典几何来说,‘自相似性’显得太简单平凡了,没有什么特别的新意,我们并不重视它。
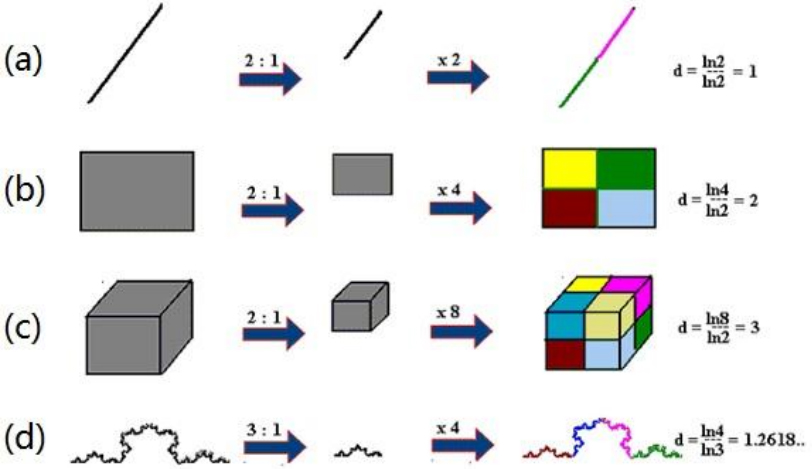
图三
不过现在,我们可以利用这种‘自相似性’,重新定义几何图形的‘维数’。
仍然利用上面的图,用自相似性来定义的‘维数’可以如此简单而直观地理解:首先将图形按照(N: 1)的比例缩小,然后,如果原来的图形 可以由(M)个缩小之后的图形拼成的话,这个图形的‘维数’d ,就等于 ln(M)/ln(N)。不难看出,将上述方法用来分析直线、平面、空间,分别得到d = 1、2、3(上图中的a、b、c)。
上图中的(d),是一种很简单的分形,叫做科和曲线,也是一种自相似图形,它的迭代生成过程如下图所示。
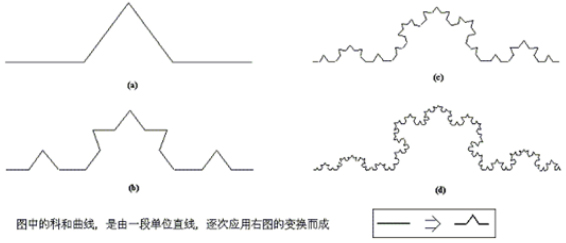
图四
可以用同样的方法分析如图(d)及上图所示的科和曲线:首先,将科和曲线的尺寸缩小至三分之一;然后,用四个这样的‘小科和曲线’,便能构成与原来一模一样的科和曲线。因此,我们得到科和曲线的维数d = ln(4)/ln(3) = 1.2618..。这就说明了,科和曲线的维数不是一个整数,而是一个小数,或分数。
下面,我们再回头研究分形龙的维数(图二)。将图中的分形龙曲线,尺寸缩小为原来的一半之后,得到右上图的小分形龙曲线。然后,将四个小分形龙曲线,分别旋转方向,成为如右下图的位置。最后,再按照右下图中箭头所指的方向,移动四个小分形龙曲线,便拼成了左下图的、与原来曲线一样的分形龙曲线。因此,如此可以证明,分形龙曲线的维数为2,因为(d = ln(4)/ln(2) = 2)。
有趣的是,分形龙图形的边界也是一个可以用迭代法产生的分形:
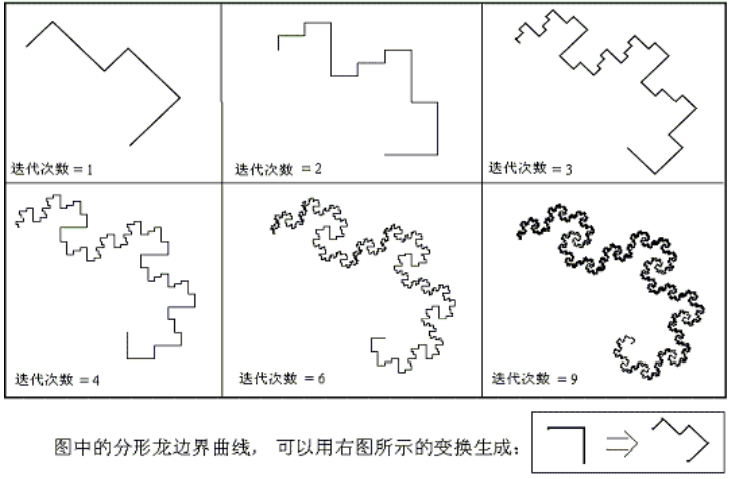
图五
由图六可知,整个分形龙曲线的边界是由四段相似的图形组成的。这种分形的维数估算方法比较复杂一些,它的“分形维数“(d)可以通过解如下方程求得:
2×2(-3/2)d + 2(-1/2)d = 1 => d = 1.523627085

图六
通过分形龙,我们认识了分形,理解了分数维。分形几何是理解混沌概念及非线性动力学的基础,在现代科学技术中,有着广泛的应用。


