——近代数学在航天飞行中的应用
小时候常常拿着星座图对着天空找星星。浩瀚的太空充满了神秘,令人向往。对大多数爱好科 学的青少年来说,星际旅行都是永恒的幻想之一。星球大战的科幻片把这些幻想实现在银幕上。随便一个按钮就是WARP速度,神奇无比。当然,实际的情况并不是那么容易。别说恒星之间的旅行,能游一游太阳系就已经很了不起了。上世纪60年代末美国把人送上了月球,算是迈出了第一步。阿姆斯壮的名言“一个人的一 小步,全人类的一大步”(One small step for a man; one giant leap for mankind.)传遍全球。后来美国又把机器探测器送上了火星。人类开始向更远的地方迈步了。
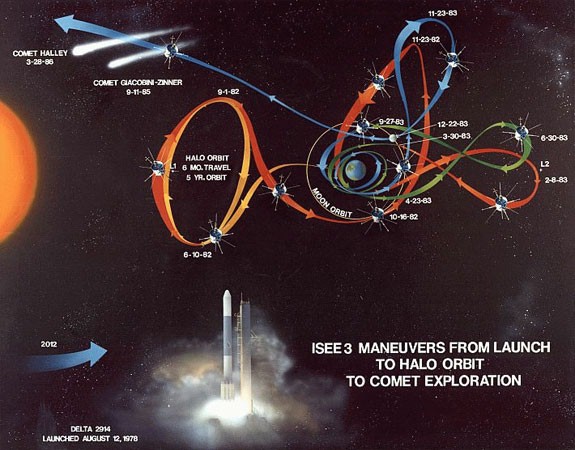
远距离航天的最大问题之一就是燃料问题。这不仅是来回的燃料,有时还有在远处几个星体之间穿行的燃料。比如访问木星。木星有好多卫星。木星的一些卫星上被发现有水,说不定可以居住。所以对木星的卫星的研究很重要,对它的每一个卫星我们都想观测,从一个卫星到另一个卫星如果完全靠燃料,则需要很多,总不能观测完一个就回地球来加油。木星离我们太远,跑一趟要好几年的时间。如何解决燃料问题就成了太空飞行的当务之急。这本来是一个物理问题,没想到竟然在近代数学的动力体系理论中找到了解。根据动力体系的理论,太空中各星体产生的重力场在各星体间有“转送带”。从一个星体到另一个星体几乎不需要燃料。靠着引力传送,坐地日行八万里。这并不是天方夜谈,而是已经经过实践验证的事实。这篇文章的目的就是要把这个“传送带”的原理作一个简单的介绍。
对于航天飞行,过去人们都单纯地只考虑二体问题。从地球出发,这二体就是飞船和地球。到达月球,这二体就是飞船与月球。要从地球到月球,根据二点之间直线距离最短的原则,出了地球轨道就径直向月球飞去。后来考虑三体问题,甚至多体问题,人们意识到我们可以借助太空中星体的引力场来省油,距离最短不见得最省燃料。在现实生活中,我们出门开车,稍微远一点就几乎肯定不会走最短线,而是走高速公路。前面提到的这些传送带就相当于星际之间的高速公路(见下图),而且这些高速公路不仅不收费,连汽油都不用,所以我把它们称为“传送带”。这些传送带是怎么形成的呢?

初中物理告诉我们,每个物体都受万有引力作用。我们处在地球,地球的引力最大,一切都只考虑地球的引力。当然,也有受别的引力影响的例子。比如海水的潮汐就受月球引力的影响,而我们地球本身的运行又主要是受太阳引力的影响。各个星体的万有引力在太空中形成一个重力场。每个星体运行几乎完全受这个重力场影响。靠近某个星体,该星体的引力就起主要作用,离它远一点,重力就小一点。现在我们考虑地球重心与月球重心的连线。离地球近的时候地球引力大,离月球近的时候月球引力大。中间必有一点两边重力相等,这一点叫不动点。实际上,由于地球和月球都在动,这一点也在跟着动,只不过相对位置不动而已。我们这里只是在地球重心与月球重心的连线上考虑,放宽到整个三维空间,实际上有一个经过这一点的曲面,这曲面上月球与地球的重力相等。如果飞船在这个曲面上运行,即不会掉向地球,也不会掉向月球。当然,飞船只是在重心连线方向上不受地球和月球的重力影响。在垂直于连线的方向上仍然受其影响。如果它在连线之上,则地球与月球的合力把它向下拉,反之,则向上拉。同样,前后也有这样的影响。似乎是在这个不动点上有一个星体在吸引它做向心运动。事实上,采集太阳风的飞船GENESIS就绕着太阳与地球之间这个质量为零的不动点转了两年多收集各种材料和情报,最后才回到地球。如果没有理论的研究,怎么能想象得出一个飞船会绕着一个空点转圈。飞船成了这个空点的卫星,这个轨道被称为光环轨道。象这样通过纯粹的理论研究然后在天体实践中得到验证,相当于上世纪初利用日食时观测到的星光弯曲来验证相对论,同样的令人惊叹。
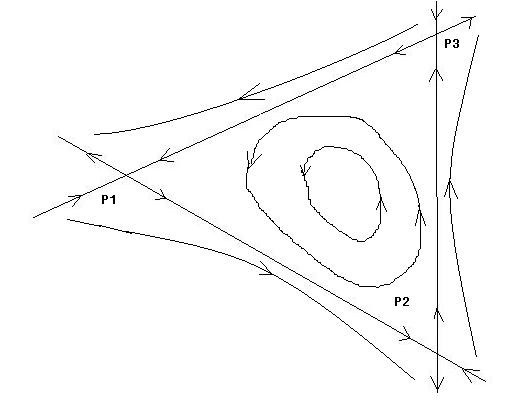
虽然这个空点有类似于“引力”的作用,但是,与一个有质量的星体不同,这个点它并不是在所有方向上都有“向心”的引力。在重心连线上它实际上相当于有排斥着用。靠地球方的掉向地球,靠月球方的掉向月球。这种同时有吸引和排斥作用的点,有时又被称为胺鞍点。数学家们对这种鞍点有过很深的研究。由这种鞍点引出来的不变曲线或曲面,在吸引方向上叫稳定流形,在排斥方向上叫不稳定流形。在太空中这些 流形的表现行式就是一个个管道。
围绕两个天体与此相似的平衡点还有四个。我们前面讲的是L1,其它点依次被记为L2,L3,L4,L5。有兴趣的读者可以到维基LAGRANGE POINT条下读到更多有关它们的特性。一个很重要的发现是,太空中由这些点的稳定与不稳定流形管道组成一个网络。飞船在这些管道中飞行,只需要借助引力而不需要任何燃料就可以从一个点附近飞到另一个点附近。做一些小小的方向操作(用一些燃料),又可以搭上另一个管道去另一个点。这样在太空中穿行,虽然不一定省时间,但更省燃料。这些平衡点仿佛成了这些高速公路的中转站。
数学家们在研究这些体系的时候,有时为了几何直观或便于讨论,把三维的问题通过一些变换(比如用庞加莱映射)化成两维问题来研究。我们可以用下面这个两维图来解释一下走远路省燃料的问题。假设要想从平衡点P1走到P3,如果走最短直线,则是逆着重力场走,要费很多燃料。如果沿着重力场管道从P1走到P2附近,通过小方向操作,再搭上通往P3的管道,就可以几乎不用燃料从P1到 P3了。
这套太空管道网络理论不仅仅是纸上谈兵,而是已经被用于实践。上世纪90年代初,日本曾送出两个飞船去观测月球。原定计划是A飞船留在地球轨道上作信号传递工作,B飞船去月球轨道。但由于技术问题,B飞船没能进入月球轨道。如果直接从地球轨道送A飞船去月球轨道,A飞船燃料不够。于是JPL实验室的人为A飞船设计了一条利用管道网络走远路去月球的方案,成功地把A飞船送到了月球轨道,使日本成了全球第三个把飞船送到月球轨道的国家。
目前,美国正在设计一个在木星各卫星之间利用管道穿行的方案,从而使飞船不用返回地球加燃料,直接在木星各卫星之间跳来跳去做观测。
中国的神舟七号已经上天了,以后还会有八号,九号。还会去月球,去火星,木星。这方面的研究人员可以大派用场。有志青年可以在这方面多做研究,把飞船送向太空深处,实现“巡天遥看一天河”的梦想。
2009年10月31日于波士顿
参考文献:
Dynamical Systems, the Three-Body Problem and Space Mission Design
http://en.wikipedia.org/wiki/Lagrange_point


