和老婆逛商场的时候,如果发现有一堆人围在某一个柜台前,老婆总是会拉着我凑上去看一看是否有便宜的东西出售。在生活中,这类行为很常见,从吃什么饭,炒什么股、到选择职业、选择居住城市,甚至在城市中过马路也乘着人多的时候过。
这种“跟风”行为的理论依据在18 世纪已经由法国的政治家Nicolas de Condorcet 给出。他设想了如下一个简单的投票模型:一个小组有100个成员,每个成员可以独立在两个方案中做选择,其中只有一个是正确的。假定每个成员对于这两个方案有一个初步的认识,选择到正确方案的几率稍大于一半(比如为0.6)。那么根据民主政治中的多数原则,小组的选择与多数人的选择一致,那么这个小组有多大的可能选择到正确的方案?
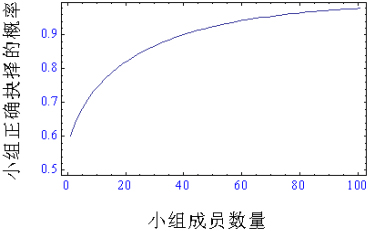
Condorcet 理论。横轴是小组成员的数量,纵轴是根据多数原则确定的小组选择正确的概率,假设了个人正确选择的概率为0.6。(函数曲线的公式在文末)
从图中可以看出,虽然个人因为能力有限,作出正确选择的概率只是略微大于胡乱的猜测。但随着小组人数的增加,小组做出正确选择的几率在不断增加。当小组人数达到100左右时,根据多数原则确定的小组选择几乎是100%正确了。
很多动物,尤其是喜欢群居的动物,也同样存在着这种“跟风”行为。动物的“跟风”是生存竞争的进化结果,其面临的是生存还是死亡的问题,因此其机制也更加精巧一些。“围观”的动物除了喜欢与大多数的选择保持一致外,更进一步还有一个所谓的“阈值响应”机制(quorum sensing)——只有当作出某种选择的同伴达到一定的数量,即所谓的“阈值”,才对这个动物个体的选择产生显著的影响(超过了线性关系)。如果低于这个“阈值”,对该动物是否参与影响不大。
在2006 年,比利时布鲁塞尔自由大学的Amé 博士所在的研究小组在蟑螂中发现了“阈值响应”的存在。他们的这项研究是实验加上理论的工作。他们把一定数量的蟑螂放到一个较大的圆盘中,在圆盘中对称的两个地方放上了两个相同的塑料瓶盖当作遮蔽点。在这个实验中,研究人员发现开始的时刻,蟑螂在圆盘中随机的走动,如果碰到了瓶盖,他们会在这个遮蔽点停留,停留的时间首先取决于这个遮蔽点的质量,如果两个遮蔽点有差别,蟑螂会在较暗的遮蔽点多停留一段时间。因为在这个实验中,两个瓶盖完全一样,所以遮蔽点的差异效应可以排除。研究人员发现,当某个遮蔽点同伴的数量超过某一个“阈值”的时候,对前来探察的蟑螂的吸引力会大大加强,而当同伴的数量小于这个“阈值”的时候,对这个探察的蟑螂的吸引力会大大的减弱。这个“阈值”的大小与蟑螂的种类,遮蔽点的容量有关。
根据这个观察,这个小组的研究人员建立了一个数学模型,经过数学的理论演算,得到了如下的预言。1,如果蟑螂的数量大于两个遮蔽点的容量,那么两个遮蔽点都会被蟑螂沾满,剩下的呆在遮蔽点外。2,如果蟑螂的数量小于一个遮蔽点的容量,那么所有的蟑螂都会栖息在一个遮蔽点。最有趣的是3,如果蟑螂的数量大于一个遮蔽点的容量而小于两个遮蔽点的容量,那么在理论上会出现的稳定的结果是蟑螂平均分配到两个遮蔽点。这个理论的结果只是数学游戏吗?在紧接着的实验中,这个小组的研究人员按照设想的这三个条件,放入适当数量的蟑螂,发现实验的结果与理论预言的结果在实验误差的范围内完全吻合。
可能你会对这个理论还有些疑虑,因为“阈值”响应本质上是“正反馈”的。简单的说:围观的人越多,导致围观点的吸引力越大,然后会导致更多的人参与围观,在理论上这个过程可以无限制的进行,最后的结果当然是系统崩溃。正反馈存在于很多的人工,自然,或者社会系统中,是系统工程师很讨厌的东西。因为这种机制会把一个不起眼的小错误给无限放大,结果导致最后系统瘫痪。对于上述实验中的第三种情况,即蟑螂的数量大于一个遮蔽点的容量而小于两个遮蔽点的容量,更可能出现的情况似乎是所有的蟑螂聚集到一个遮蔽点,其余的容纳不下的进入第二个遮蔽点。出现这种结果的原因是因为蟑螂除了喜欢群聚外,也害怕拥挤。如果一个遮蔽点蟑螂的数量过多,也会减少对巡游蟑螂的吸引力,呈现一种线性关系。在这个模型中,正是这个害怕拥挤的线性效应平和了“阈值响应”,导致出现了上述的第三种结果。
这种“阈值响应”在蟑螂寻找遮蔽点的过程中存在,在蚂蚁觅食的路径的形成,在蜜蜂寻找新的筑巢点的过程中也存在,甚至在一些脊椎动物,如三刺鱼(three-spine stickleback)中也存在。如此看来,“跟风”这种现象,实际上蕴藏着古老的智慧。早在人类之前,动物严酷的生存竞争中就学会了这种策略,而且做了大大的改进。
附录:Condorcet 理论,计算小组做出正确选择的概率。
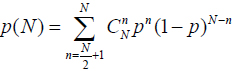
N 是小组的总人数,n 是做出正确选择的人数,p是个体做出正确选择的概率,![]() 是从总人数N中选出n个个体的排列数。
是从总人数N中选出n个个体的排列数。
作者:胡锋, 理论物理博士。 重庆市沙坪坝区天陈路12 号 400047 重庆师范大学物理与电子工程学院教师


